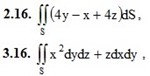ИДЗ 15.1 – Вариант 16. Решения Рябушко А.П.
Содержимое: 16v-IDZ15.1.doc (201.00 KB)
Загружен: 09.11.2016
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 3
Возвраты: 0
120 руб.
1. Дана функция u(M) = u(x, y, z) и точки M1, M2. Вычислить: 1) производную этой функции в точке M1 по направлению вектора M1M2; 2) grad u(M1)
1.16. u(M) = ln(x3 + y3 + z + 1), M1(1, 3, 0), M2(–4, 1, 3)
2. Вычислить поверхностный интеграл первого рода по поверхности S, где S – часть плоскости (p), отсеченная координатными плоскостями.
(p): x – 2y + 2z = 2
3. Вычислить поверхностный интеграл второго рода.
где S – часть поверхности параболоида z = x2 + y2 (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью z = 4.
4. Вычислить поток векторного поля a(M) через внешнюю поверхность пирамиды, образуемую плоскостью (p) и координатными плоскостями, двумя способами: а) использовав определение потока; б) с помощью формулы Остроградского – Гаусса.
4.16. а(M) = 4zi + (x – y – z)j + (3y + z)k, (p): x – 2y + 2z = 2
1.16. u(M) = ln(x3 + y3 + z + 1), M1(1, 3, 0), M2(–4, 1, 3)
2. Вычислить поверхностный интеграл первого рода по поверхности S, где S – часть плоскости (p), отсеченная координатными плоскостями.
(p): x – 2y + 2z = 2
3. Вычислить поверхностный интеграл второго рода.
где S – часть поверхности параболоида z = x2 + y2 (нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостью z = 4.
4. Вычислить поток векторного поля a(M) через внешнюю поверхность пирамиды, образуемую плоскостью (p) и координатными плоскостями, двумя способами: а) использовав определение потока; б) с помощью формулы Остроградского – Гаусса.
4.16. а(M) = 4zi + (x – y – z)j + (3y + z)k, (p): x – 2y + 2z = 2
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Отзывов от покупателей не поступало